Innerhalb dieses Systems stellt die Ebenheit eine grundlegende Steuerung der Form dar, die dafür verwendet wird zu bestimmen, wie gerade eine Oberfläche über eine 2D-Ebene hinweg verläuft. Die Formtoleranzen bestehen dabei in der Geometrischen Bemaßung und Tolerierung aus die Form steuernden Beschriftungen, sog. „Callouts“, wie Geradheit, Ebenheit, Rundheit und Zylindrizität.
Im Gegensatz zur Lage- oder Ausrichtungssteuerung erfordert die Formsteuerung kein Datum bzw. Bezugspunkt als Referenz; sie wird direkt auf die Form des Elements selbst angewendet.
Was ist die Ebenheit in GD&T?
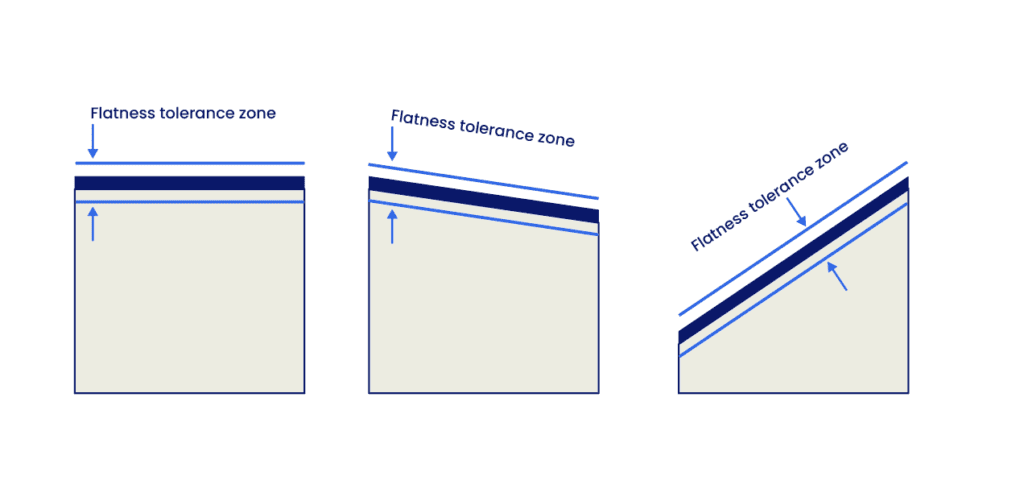
Die Ebenheit, oder auch Flachheit, als Toleranz steuert die Planarität einer Oberfläche. Sie definiert dabei einen Toleranzbereich, der aus zwei zueinander parallelen Ebenen besteht, die entsprechend dem Toleranzwert voneinander entfernt sind. Alle Punkte der tatsächlichen Oberfläche müssen dabei zwischen diesen zwei Ebenen liegen.
Der Toleranzbereich, die Toleranzzone, schwebt dabei frei. Die Ebenen an sich müssen dabei nicht zwingend parallel zu einer anderen Oberfläche oder einem Datum sein; sie werden allein durch die Oberfläche definiert, die sie steuern sollen.
Die Ebenheitstoleranz definiert dabei, wie eben bzw. flach eine Oberfläche ist, und stellt sicher, dass die höchsten und niedrigsten Punkte einer Oberfläche innerhalb der spezifizierten Toleranzzone liegen.
Das Callout, die Beschriftung, für die Ebenheit kann außerdem dazu verwendet werden, um ein Merkmal der Größe zu steuern, zu fertigen und danach zu prüfen[1]. In diesem Fall bemisst das Callout in der Tat eine Abweichung von der abgeleiteten Meridianebene.
Die Ebenheit wird hauptsächlich dafür eingesetzt, eine Referenzfläche (ein sog. Datum) zu kontrollieren oder die Genauigkeit der Präzision anderer Toleranzen zu erhöhen, was es kritischen Passflächen erlaubt eine ausreichende Abdichtung, Schmierung, Spannungsaufkonzentration und Lastenverteilung zu gewährleisten, ohne die Toleranzen weiter einzuschränken.
Merkmalskontrollrahmen (FCF) für die Ebenheitstoleranz
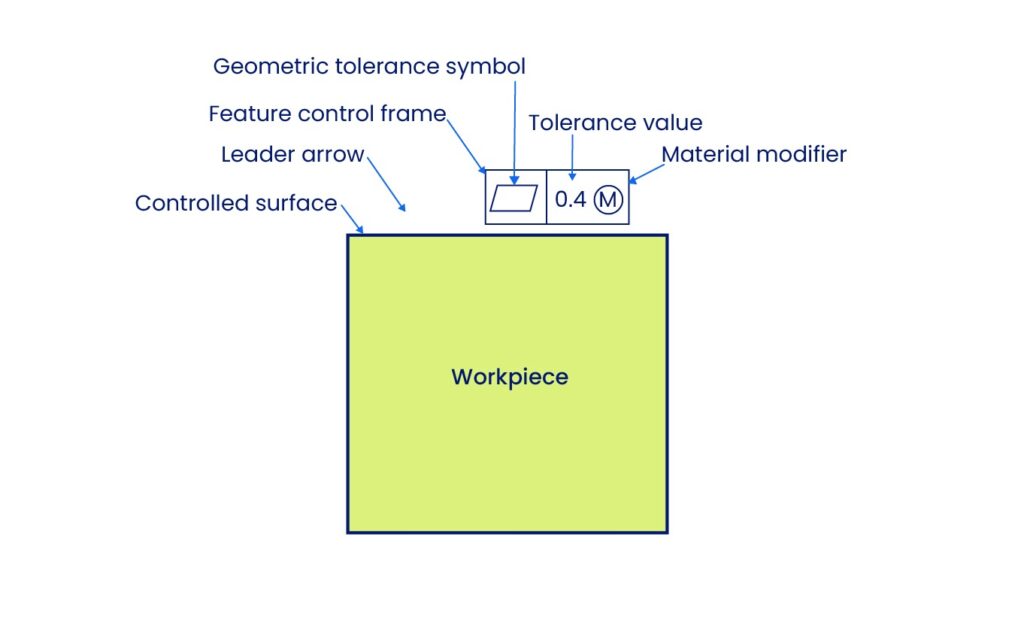
Der Merkmalskontrollrahmen, im Englischen Feature Control Frame – FCF, für die Ebenheit ist ein rechteckiger Kasten, der in spezifische Bereiche, sog. Fächer, unterteilt wird, die die Anforderungen an die Toleranz definieren.
- Erstes Fach (Symbol): Beinhaltet das Symbol des geometrischen Merkmals. Für Ebenheit ist dies ein Parallelogramm.
- Zweites Fache (Toleranzwert): Spezifiziert die zulässige Gesamtabweichung. Dieser Zahlenwert definiert dabei den Abstand zwischen den beiden parallelen Ebenen der Toleranzzone.
- Keine Datumsreferenz: Da die Ebenheit eine von anderen Merkmalen unabhängige Formularsteuerung darstellt, gibt es kein drittes Fach für die Bezugsreferenz.
Platzierung des Führungspfeils: Die Platzierung des Führungspfeils ist entscheidend für die Interpretation.
- Oberflächenkontrolle: Wenn der Führungspfeil auf eine Oberfläche oder ihre Verlängerungslinie zeigt, dann steuert die Toleranz die Oberfläche an sich.
- Abgeleitete Meridianebene: Wenn der Pfeil auf die größte Bemaßung zeigt, steuert die Toleranz die abgeleitete Medianebene (die Mittelebene des Merkmals).
Designtipp: Maximieren Sie den Toleranzwert immer so weit, wie es die Funktionalität erlaubt. Unnötig enge Toleranzen erfordern teure maschinelle Bearbeitungs- und Prüfprozesse (z.B. das Schleifen oder Läppen), die die Teilkosten signifikant in die Höhe treiben.
Ebenheit vs. Andere Toleranzen
Die Ebenheit wird oft mit der Geradheit, Parallelität und Oberflächengüte verwechselt. Das Verständnis der Unterschiede ist für die Auswahl der korrekten Beschriftung entscheidend.
Ebenheit vs. Geradheit
Die Ebenheit ist eine 2D-Version der Geradheitstoleranz. Während die Geradheitstoleranz eine Toleranzzone mit zwei parallelen Linien erzeugt, besteht die Ebenheitstoleranzzone aus zwei parallelen Ebenen, sodass die Steuerung durch eine 2D-Oberfläche statt einer 1D-Linie erfolgt.
Verwenden Sie die Geradheit, um die „Welligkeit“ einer Welle oder einer einzelnen Linie auf einem Block zu steuern. Verwenden Sie hingegen die Ebenheit, um die Spitzen und Täler einer gesamten Dichtfläche oder Tischoberfläche zu steuern.
Flachheit vs. Parallelität
Der Hauptunterschied zwischen diesen beiden Steuerungsansätzen ist die Notwendigkeit eines Datums. Die Parallelität steuert die Ausrichtung einer Oberfläche in Relation zu einem spezifischen Datum, und stellt damit sicher, dass eine Ebene äquidistant zu einer anderen bleibt. Die Ebenheit hingegen ist eine unabhängige Anforderung an die Form einer einzelnen Oberfläche, die ohne Bezug (und Rücksicht) auf andere Merkmale gesteuert wird.
Verwenden Sie die Ebenheit, wenn eine Oberfläche planar sein muss, ihr Winkel in Relation zum Rest des Teils aber keine Rolle spielt (z.B. eine eigenständige Referenzplatte). Verwenden Sie die Parallelität, wenn die Oberfläche perfekt zu einer gegenüberliegenden Fläche oder einer vorgesehenen Montageebene (z.B. eine Tischplatte zum Fußboden) ausgerichtet werden soll.
Ebenheit vs. Oberflächengüte
Während beide Begriffe die Qualitäten von Oberflächen beschreiben, arbeiten Sie jedoch in unterschiedlichen Maßstäben. Die Ebenheit steuert und kontrolliert Abweichungen im Makro-Bereich wie ein Verbiegen, Verziehen oder Verdrehen. Die Güte der Oberflächenbeschaffenheit hingegen misst Unregelmäßigkeiten auf der Mikro-Ebene, insbesondere im Kontext der Rauheit der Oberflächentextur. Ein Teil kann zum Beispiel perfekt flach sein, aber rau, während ein anderes Teil spiegelnd poliert (glatt) und dennoch verzogen sein kann.
Nutzen Sie die Ebenheit um sicherzustellen, dass die Teile während der Montage korrekt zusammenpassen. Nutzen Sie die Oberflächengüte, um subtilere Interaktionen wie Reibung, Verschleißraten oder die Dichtigkeit zu kontrollieren.
Wie die Ebenheitstoleranz gemessen wird
Die Überprüfung der Ebenheit erfordert spezielle Messwerkzeuge, die auf der Grundlage der Enge der Toleranz, der für die Prüfung verfügbaren Zeit und der dabei erforderlichen Genauigkeit ausgewählt werden. Während es verschiedene fortgeschrittene Verfahren gibt, so sind die drei häufigsten Methoden in der Fertigung: Höhenmesser mit Messuhren, Koordinatenmessgeräte (KMG) sowie die optische Laserinterferometrie.
1. Höhenmesser mit Messuhr
Die manuelle Messung mit einer Messuhr ist der Standardansatz in Fabriken und Werkstätten. Es gibt dafür drei unterschiedliche Techniken zur Durchführung, die alle individuelle Genauigkeits- und Einrichtungsansprüche mit sich bringen.
Die Oberflächenplattenmethode (Schnelltest): Das am häufigsten im Alltag eingesetzte Verfahren besteht darin, das Teil direkt auf eine Präzisionsoberflächenplatte zu legen, die Messuhr auf der Oberfläche auf Null zu stellen, und dann damit über das Teil zu streichen. Die Different zwischen dem Maximal- und Minimalwert stellt dabei dann die Gesamtabweichung dar.
Während das eine schnelle und bequeme Möglichkeit zur Überprüfung eines Teils ist, so misst man damit so gesehen die Parallelität und nicht nur die Ebenheit. Da das Teil auf der Fläche der Präzisionsplatte aufliegt, agiert die Platte als Datum; womit jeder Winkel auf der (nicht mit der Uhr gemessenen) Unterseite des Teils die Anzeige auf der Oberseite beeinflusst. Weil die Ebenheit jedoch eine unabhängige Anforderung darstellt, bedeutet es, dass die Oberfläche nicht zwingend parallel zum Untergrund sein muss, und somit die Methode für viele Szenarien ein praktische „Schnelltest“ ist.
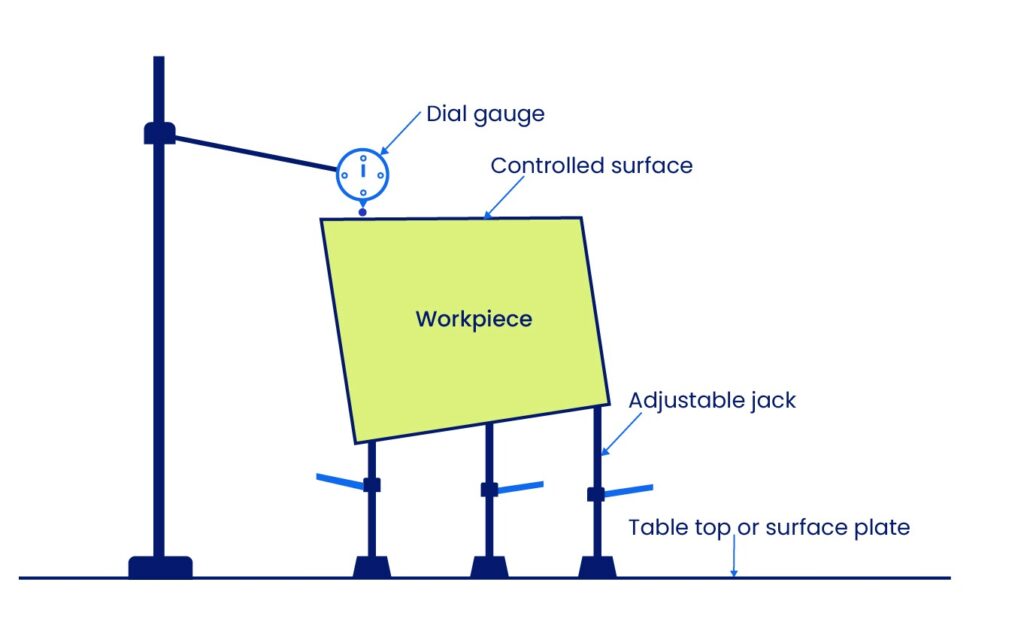
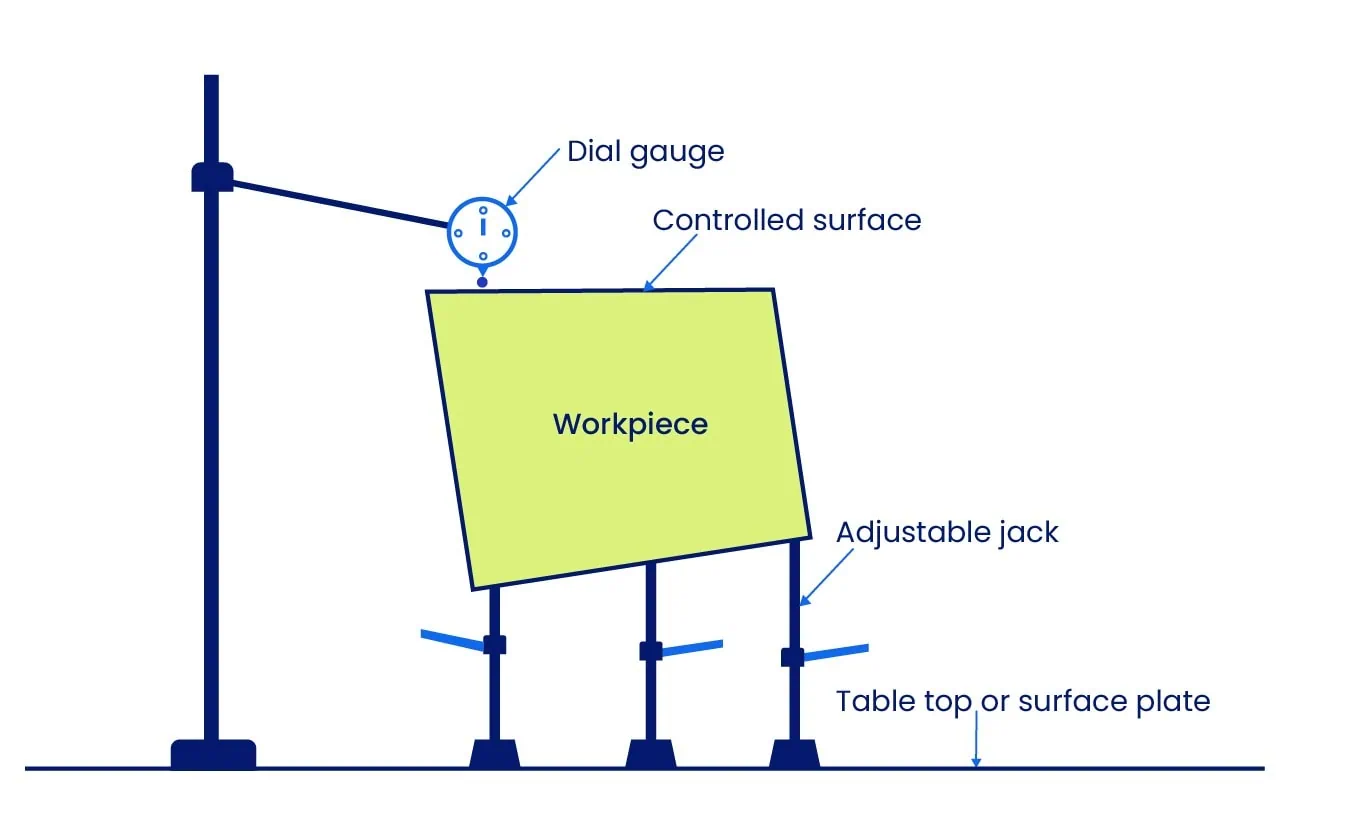
Die 3-Punkt-Ständer-Methode (Empfohlen): Für eine höhere Genauigkeit empfehlen wir die zu kontrollierende Oberfläche von der Einwirkung der Unterseite zu isolieren. Dies wird dadurch erreicht, dass das Werkstück mit der zu kontrollierenden Oberfläche nach oben auf drei anpassbaren Ständern platziert wird.
Bei der Prüfung wird die Messuhr an den Punkten direkt über den Ständern auf Null gesetzt. Durch die individuelle Höhenverstellung der Ständer werden alle drei Punkte zueinander auf Null gebracht, wodurch eine virtuelle Ebene parallel zur Oberfläche erzeugt wird. Nach diesem Nivellieren fährt der Prüfer die Oberfläche mit der Messuhr ab; die Differenz zwischen dem höchsten und niedrigsten Punkte stellte dann die Ebenheitsabweichung dar.
Diese Methode ist zeitaufwändiger, bietet jedoch eine überragende Genauigkeit, indem eine echte Ebenheitstoleranzzone unabhängig von der Auflagefläche und Unterseite festgelegt wird.
Die Kopfüber-Methode: Eine dritte Alternative ist die „Face-Down“ – Methode, bei der die zu kontrollierende Oberfläche auf eine Oberflächenplatte mit einem Loch in der Mitte gelegt wird. Die Messuhr wird dann von unten, durch das Loch hindurch, auf der zu prüfenden Oberfläche eingesetzt. Diese Methode ist zwar genau, hat jedoch einen erheblichen Nachteil: Der Prüfer muss das Werkstück bewegen, um die gesamte Oberfläche abzutasten. Durch die Bewegung des Teils können sich jedoch die oberflächenspezifischen Höhenpunkte, die als Kontaktpunkt auf der Oberflächenplatte aufliegen, verändern, was zu lageabhängigen Fehlern führen kann.
2. Einsatz eines Koordinatenmessgerätes (KMG)
Bei komplexen Teilen, oder im Rahmen automatischer Prüfungen, ist eine KMG in der Lage, eine hochpräzise Ebenheitsmessung durchzuführen. Während die Softwareschnittstellen bzw. ihre Oberflächen variieren, so beinhaltet das Messverfahren im Allgemeinen das Importieren von mindestens drei orthogonalen Oberflächen (mit jeweils vier Punkten), um die Achsen eines Koordinatensystems (X, Y, Z) zu definieren.
Die KMG-Software berechnet dann aus diesen Ebenen die Hüllkurve der Ebenheitstoleranzzone, die aus den beiden parallelen Ebenen besteht, zwischen denen alle Punkte der zu kontrollierenden Oberfläche liegen müssen. Die Prüfsonde zeichnet ein definiertes Raster von Prüfpunkten ab; eine größere Zahl an Messpunkten mit einer gründlichen Verteilung liefert dabei ein genaueres Ergebnis.
Ein wesentlicher Vorteil eines KMG ist die Fähigkeit Merkmale der Größe zu messen. Es kann somit beide Seiten eines Teils sondieren, um dann daraus mathematisch eine Abgeleitete Medianebene zu erzeugen, anhand derer sie dann die Ebenheit dieser imaginären Mittelebene bestimmt. Dies ist mit manuellen Messuhren nicht möglich.
3. Einsatz optischer Methoden (Laserinterferometrie)
Für die Messung extrem enger Toleranzen bis hinunter auf die nanoskalare Ebene ist die Laserinterferometrie der Standard. Sie ist eine berührungslose Methode, die sich ideal für große Teile eignet, die mit herkömmlichen Werkzeugen nicht gemessen werden können, oder für empfindliche Teile, die sich bereits durch den Kontakt mit der Sonde verformen könnten.
Das Verfahren wertet die Interferenzmuster zweier kohärenter Lichtstrahlen aus, um die Schwankungen in der Entfernung auf der Oberfläche zu berechnen. Während dies zwar die genaueste der genannten Methoden darstellt, hat sie jedoch auch Grenzen. Es sind im Allgemeinen reflektierende Oberflächen nötig, und das Verfahren ist sehr empfindlich gegenüber Umgebungsgeräuschen, Vibrationen und Luftturbulenzen.
Der Zusammenhang zwischen Ebenheitstoleranzen und Größentoleranzen
Das Verständnis der Hierarchie zwischen Größe und Form ist entscheidend für die Erzeugung gültiger Konstruktionszeichnungen. Es gibt dazu zwei unterschiedliche Anwendungsszenarien: Standardanwendungen (Ebenheit der Oberfläche) und Anwendungen mit Materialmodifikatoren (Größenmerkmale).
Die Allgemeine Regel: Ebenheit ≤ Größe
Entsprechend des sog. Hüllprinzips („Envelop Principle“ gem. ASME Y14.5), darf die Form eines Merkmals nie die perfekte Grenze verletzen, die durch den Maximalen Materialzustand (MMC) definiert wird. Dementsprechend darf die Ebenheitstoleranz nie größer sein als die Größentoleranz.
Würde die Ebenheitstoleranz größer als die Größentoleranz definiert, entstünde daraus ein logischer Widerspruch. So könnte man zum Beispiel eine Platte betrachten, die eine Toleranz für ihre Dicke von 10 ± 0,2 mm aufweist. (Gesamtgrößentoleranz = 0,4 mm) Würde man nun eine Ebenheitstoleranz von 0,5 mm ansetzen, so wäre es für das Teil unmöglich die Größenbeschränkungen einzuhalten (also sich im Rahmen der Hüllkurve von 10,2 mm zu bewegen) während sich das Teil bereits um bis zu 0,5 mm verformen darf. Zeichnungen mit dieser Art Fehler führen zu widersprüchlichen Prüfergebnissen und nicht funktionsfähigen Teilen.
Ebenheitstoleranzen bei unterschiedlichen Materialtoleranzen und Bonustoleranzen
Die Ausnahme: Bonustoleranzen mit Materialmodifikatoren
Die einzige Ausnahme zu der oben genannten Regel stellt die Ebenheit dar, wenn sie auf ein Merkmal der Größe (Abgeleitete Medianebene) mit einem Materialmodifikator angewendet wird. In diesem Szenario würde die Größentoleranz die lokalen Abmessungen steuern, während die Ebenheitstoleranz die Form unabhängig davon steuert.
Der Einsatz des Maximalen Materialzustands (M) oder des Minimalen Materialzustands (L) erlaubt die Verwendung von Bonustoleranzen. Dies bedeutet, dass sich die Ebenheitstoleranz dynamisch erhöhen kann, wenn die tatsächliche Größe des Teils von der spezifizierten Bedingung abweicht, den Herstellern eine größere Flexibilität ohne Kompromisse bei der Funktion erlaubt.
1. Ebenheit mit MMC und Bonustoleranz Der maximale Materialzustand (MMC) stellt sicher, dass die Teile selbst dann zusammen passen, wenn ein Worst-Case-Szenario vorliegt. Stellen Sie sich eine Oberfläche mit einer Größentoleranz von 100 ± 0,4 mm vor. Ihre MMC-Größe (die maximal zulässige Größe) ist 100,4 mm.
Wenn wir nun eine Ebenheitstoleranz von 0,3 mm anwenden, gilt diese Toleranz auch dann, wenn das Teile seine maximale Größe (im Sinne der MMC) hat. Wird das Teil jedoch kleiner gefertigt (von der MMC aus in Richtung LMC), wird die Passung lockerer. Diesen „zusätzlichen Platz“ kann man nun nutzen, um die Ebenheitstoleranz zu erhöhen, ohne dass die Montage dadurch beeinträchtigt werden kann.
Diese Reduzierung der tatsächlichen Größe von der MMC weg wird zur Ebenheitstoleranz addiert. Dieser zusätzliche „Spielraum“ nennt sich Bonustoleranz.
- Beispielrechnung: Falls die tatsächlich gefertigte Größe 100 mm entspricht, (was 0,4 mm weniger sind als die MMC von 100,4 mm), erhält der Hersteller somit eine zusätzliche Toleranz von 0,4 mm.
Gesamtebenheitstoleranz = Ursprüngliche Toleranz (0,3 mm) + Bonus (0,4 mm) = 0,7 mm
Im MMC (100,4 mm) ist der Bonus 0 mm. Im LMC (99,6 mm) ist der Bonus maximal und bei 0,8 mm. Diese zusätzliche Flexibilität verringert die Fertigungskosten und den Ausschuss.
Berechnung der Bonustoleranz im MMC (Maximaler Materialzustand)
(Spezifikationen: Größe = 100 ± 0,4 mm; Ebenheit = 0,3 im MMC)
| Tatsächliche Teilgröße (mm) | Bonustoleranz (mm) | Gesamtebenheitstoleranz (mm) |
| 100,4 (im MMC) | 0 | 0.3 |
| 100.3 | 0.1 | 0.4 |
| 100.2 | 0.2 | 0.5 |
| 100.1 | 0.3 | 0.6 |
| 100.0 | 0.4 | 0.7 |
| 99.9 | 0.5 | 0.8 |
| 99.8 | 0.6 | 0.9 |
| 99.7 | 0.7 | 1.0 |
| 99,6 (im LMC) | 0.8 | 1.1 |
Ebenheit mit LMC und Bonustoleranz
Der Minimale Materialzustand (LMC) wird für bestimmte Sicherheits- und Funktionsanforderungen eingesetzt, wie z.B. für die Einhaltung einer Mindestwandstärke für Druckbehälter. Während der MMC für einen festen Sitz sorgt, stellt der LMC sicher, dass die Teile nicht zu dünn oder zu schwach werden.
Für den Einsatz des LMC wird die Bonustoleranzrechnung umgekehrt. Diese Toleranz gilt streng für die LMC-Größe (die kleinste erlaubte Größe). Wenn das Teil größer gefertigt wird (es sich vom LMC weg nach obeb zum MMC hin bewegt), so erhält der Hersteller eine Bonustoleranz.
Die Größe der Bonustoleranz ist die Differenz zwischen der LMC-Größe und der tatsächlichen Größe des Teils. Der Bonus ist somit 0, wenn das Teil im LMC ist und erreicht sein Maximum, wenn das Teil im MMC ist.
Berechnung der Bonustoleranzen im LMC
(Spezifikationen: Größe = 100 ± 0,4 mm; Ebenheit = 0,3 im LMC)
| Tatsächliche Teilgröße (mm) | Bonustoleranz (mm) | Gesamtebenheitstoleranz (mm) |
| 99,6 (im LMC) | 0 | 0.3 |
| 99.7 | 0.1 | 0.4 |
| 99.8 | 0.2 | 0.5 |
| 99.9 | 0.3 | 0.6 |
| 100.0 | 0.4 | 0.7 |
| 100.1 | 0.5 | 0.8 |
| 100.2 | 0.6 | 0.9 |
| 100.3 | 0.7 | 1.0 |
| 100,4 (im MMC) | 0.8 | 1.1 |
Glossar der wichtigsten Begriffe
| Begriff | Definition | Kontext |
| Gesamt- ebenheits- zone | Der standardisierte 3D-Toleranzbereich, der zwischen zwei parallelen Ebenen existiert. | Für die Flachheit der Oberfläche verwendet. Die gesamte Oberfläche muss zwischen diesen Ebenen liegen. |
| Merkmal der Größe | Jegliches Merkmal an einem Teil, das physikalisch gemessen werden kann (z.B. ein Loch, ein Stift, ein Schlitz oder die Plattendicke). | Wird verwendet, wenn die Ebenheit die Form eines bestimmten Maßes und nicht nur die Oberfläche steuert. |
| Abgeleitete Meridian- ebene | Eine imaginäre Linie, die berechnet wird, indem die Mittelpunkte aller gegenüberliegenden Linienelemente auf einem Merkmal verbunden werden. | Wird verwendet, wenn Ebenheit auf ein Merkmal der Größe angewendet wird (z.b. die Dicke einer Platte). |
| Bonus- toleranz | Zusätzliche Toleranz, die verfügbar wird, wenn ein Merkmal in seiner Größe von seinem Maximalen Materialzustand (MMC) nach unten hin abweicht. | Nur für die Ebenheit verfügbar, wenn diese auf ein Merkmal der Größe (M) angewendet wird. |
| Virtueller Zustand | Die kollektive, nicht materielle Grenze, die durch den kombinierten Effekt der Größe des Merkmals bei MMC und der geometrischen Toleranz erzeugt wird. | Entscheidend für die Konstruktion von Gegenstücken in Passungen, um eine ordnungsgemäße Montage sicherzustellen (z.B., dass eine Lasche in einen Schlitz passt). |
Beherrschung der Formsteuerung
Ebenheit ist eine der vielseitigsten Formen der Steuerung durch GD&T, wird aber selten isoliert eingesetzt. Um vollständig herstellbare Teile zu schaffen, müssen Ingenieure verstehen, wie die Steuerelemente mit anderen Toleranzen interagieren.
- vs. Geradheit: Wenn Sie nur ein einzelnes Linienelement auf einer Fläche und nicht die gesamte Fläche steuern müssen, verwenden Sie die Geradheit.
- vs. Parallelität: Wenn Sie nur die Ausrichtung der Oberfläche relativ zu einem Datum steuern müssen (z.B. eine Tischplatte parallel zum Boden), dann verwenden Sie die Parallelität.
- vs. Oberflächengüte: Wenn Sie die mikroskopische Rauigkeit oder die Textur einer Oberfläche statt ihrer makroskopischen Form steuern wollen, nutzen Sie die Oberflächengüte bzw. das Finish.
Für weitere Einsichten bezüglich der Steuerelemente lesen Sie unseren umfassenden Leitfaden zur Geometrischen Bemaßung und Tolerierung in der technischen Bibliothek von Xometry Pro.
 Europe
Europe  Türkiye
Türkiye  United Kingdom
United Kingdom  Global
Global 

 Anmeldung mit meinem Xometry-Konto
Anmeldung mit meinem Xometry-Konto  0
0










Comment(0)